Diskrete Dreiecksverteilung

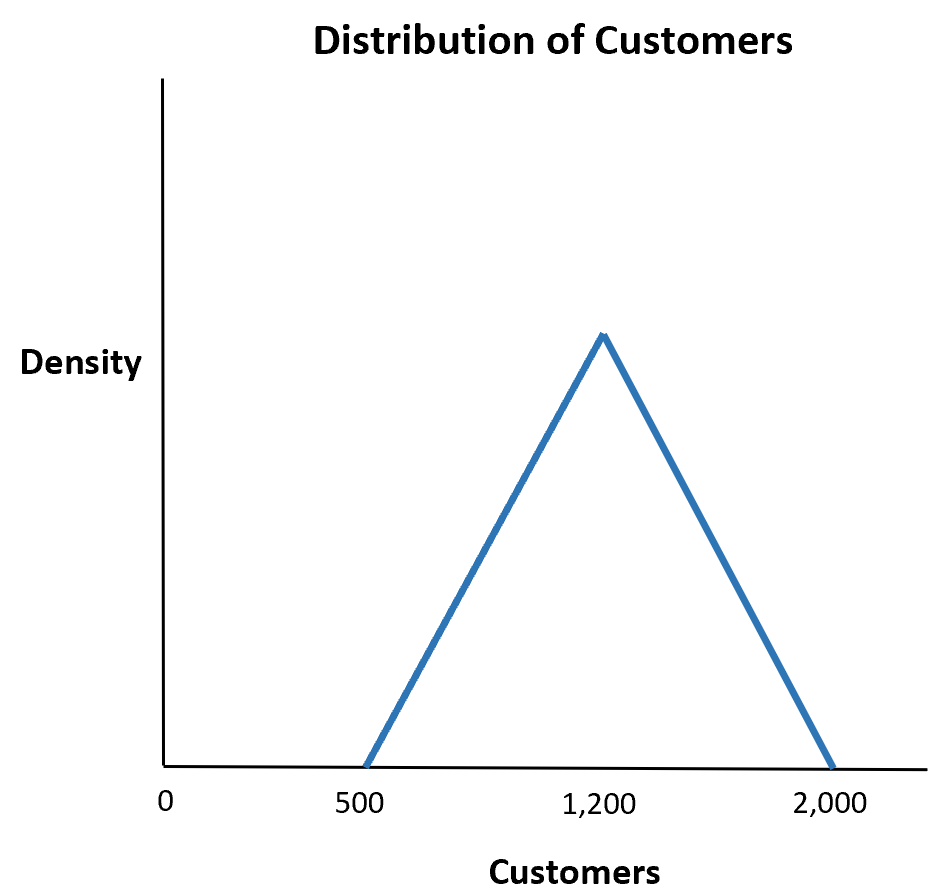
Die diskrete Dreiecksverteilung ist eine spezielle Wahrscheinlichkeitsverteilung in der Stochastik. Sie zählt zu den diskreten Wahrscheinlichkeitsverteilungen auf einer endlichen Menge und ist eine univariate Wahrscheinlichkeitsverteilung.

Typischerweise findet diese Wahrscheinlichkeitsverteilung Anwendung bei der Summe von identischen gleichverteilten Zufallsgrößen, die in einer symmetrischen Dreiecksverteilung resultiert.

Symmetrische Dreiecksverteilung

Wählt man zwei ${\displaystyle a$ mit ${\displaystyle b-a=n-1}$, so wählt man als Träger die Menge

${\displaystyle T:=\{2a,2a 1,2a 2,\dotsc ,2b-1,2b\}}$

und definiert die Wahrscheinlichkeitsfunktion für ${\displaystyle x\in \mathbb {Z} }$

${\displaystyle \operatorname {P} (X=x)=f(x)={\begin{cases}{\frac {x-2a 1}{n^{2}}}&{\text{für }}2a\leq x\leq a b\\{\frac {2b-x 1}{n^{2}}}&{\text{für }}a b\leq x\leq 2b\\0&{\text{sonst}}\end{cases}}}$

Der Erwartungswert beträgt ${\displaystyle a b}$, die Varianz ${\displaystyle \operatorname {Var} (X)={\frac {(b-a 2)(b-a)}{6}}}$ ist das Doppelte der Varianz der gleichverteilten Zufallsgröße zur Menge :${\displaystyle \{a,a 1,a 2,\dotsc ,b-1,b\}}$.

Asymmetrische Dreiecksverteilung

Die Verteilung auf der Menge :${\displaystyle T:=\{0,1,2,\dotsc ,n-1\}}$ mit

${\displaystyle \operatorname {P} (X=x)=f(x)={\begin{cases}1/n&{\text{für }}x=0\\{\frac {2n-2x}{n^{2}}}&{\text{für }}0$

ist ein diskretes Gegenstück zur stetigen Dreiecksverteilung, die sich als Betrag der Differenz gleichverteilter Zufallsgrößen ergibt.

Beispiel

Beispielsweise bei den Brettspielen Backgammon oder Siedler von Catan wird die Augensumme von zwei Würfeln betrachtet. Somit gilt ${\displaystyle a=1}$ und ${\displaystyle b=6}$. Die Augensumme ist daher symmetrisch dreiecksverteilt auf dem Träger ${\displaystyle \{2,3,\dotsc ,12\}}$, der Erwartungswert ist ${\displaystyle 1 6=7}$.

Einzelnachweise